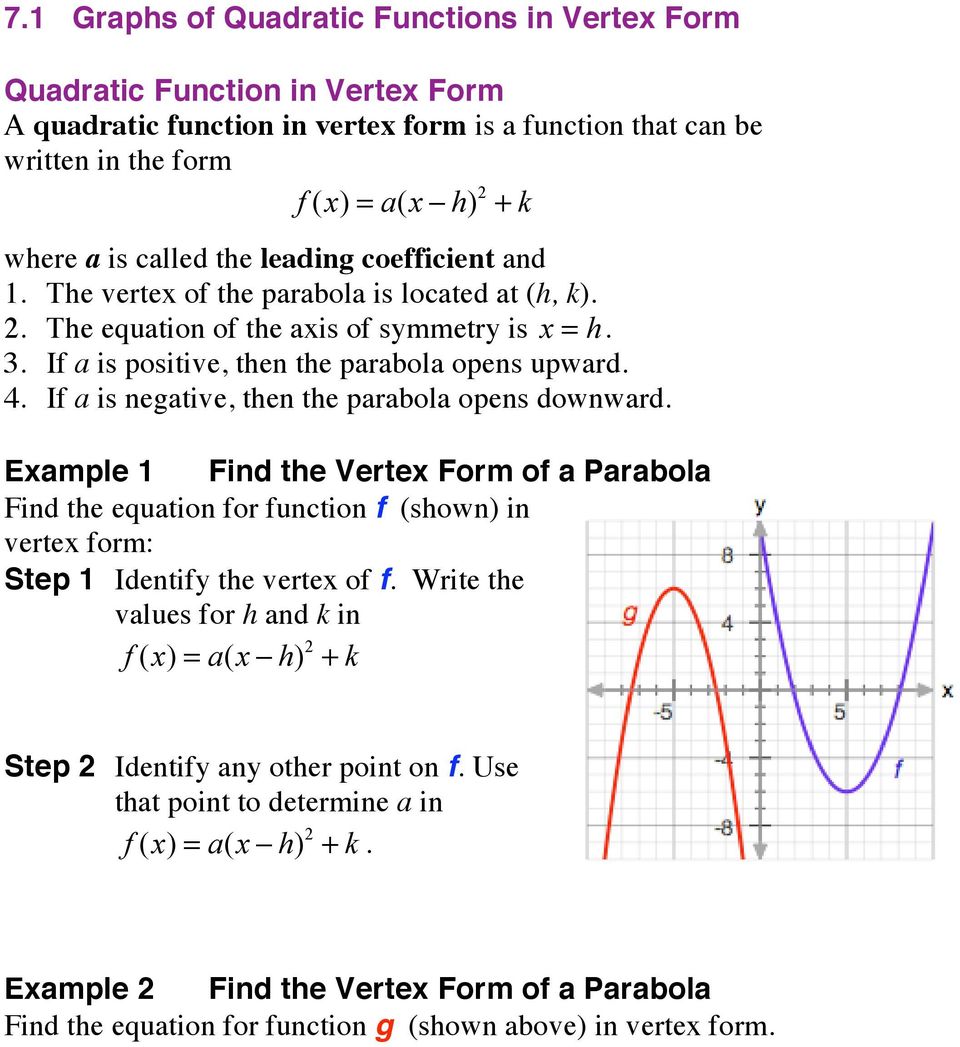
The quadratic function {eq}f(x)=a(xh)^2k {/eq} is in standard form (a) The graph of f is a parabola with vertex (x,y )=( _____) (b) If a >0, the graph of f opensTransformations of Graphs (a, h, k) Consider the function y = f (x) We're going to refer to this function as the PARENT FUNCTION The following applet allows you to select one of 4 parent functions The basic quadratic function f (x) = x^2 The basic cubic function f (x) = x^3 The basic absolute value function f (x) = x The basic squareFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor
9 8 Graph Quadratic Functions Using Transformations Mathematics Libretexts
What is the vertex of the graph f(x)=y=a(x-h)2+k
What is the vertex of the graph f(x)=y=a(x-h)2+k-Any quadratic function can be written in the standard form f (x) = a (x h) 2 k where h and k are given in terms of coefficients a , b and c Let us start with the quadratic function in general form and complete the square to rewrite it in standard form Given function f (x) f (x) = ax 2 bx c factor coefficient a out of the terms in xConsider the graph of the parabola y=ax^2 Its vertex is clearly at (0,0) Now, if you replace x with xh in any equation, its graph gets shifted to the right by a distance of h



Graphing Quadratic Equations
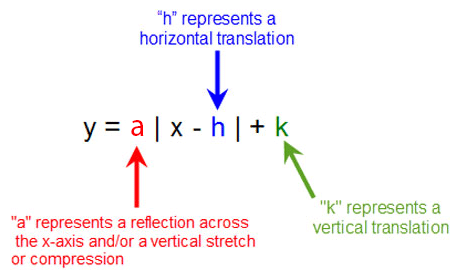
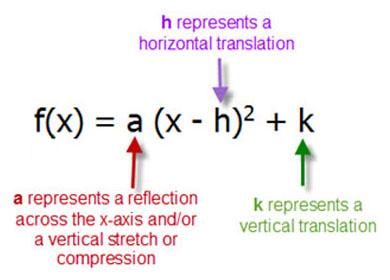
How to graph a quadratic function using transformationsThe figure shows a graph of the function $f(x)=x^2$ a) For each of the graphs of quadratic functions below, find values of $a$, $h$, and $k$ so that the function $fF(x – h) Shifts a graph right h units Add h units to x f(x h) Shifts a graph left h units Subtract h units from x f(x) k Shifts a graph up k units Add k units to y f(x) – k Shifts a graph down k units Subtract k units from y Reflections cause a graph to rotate (or flip) over the xaxis or yaxis
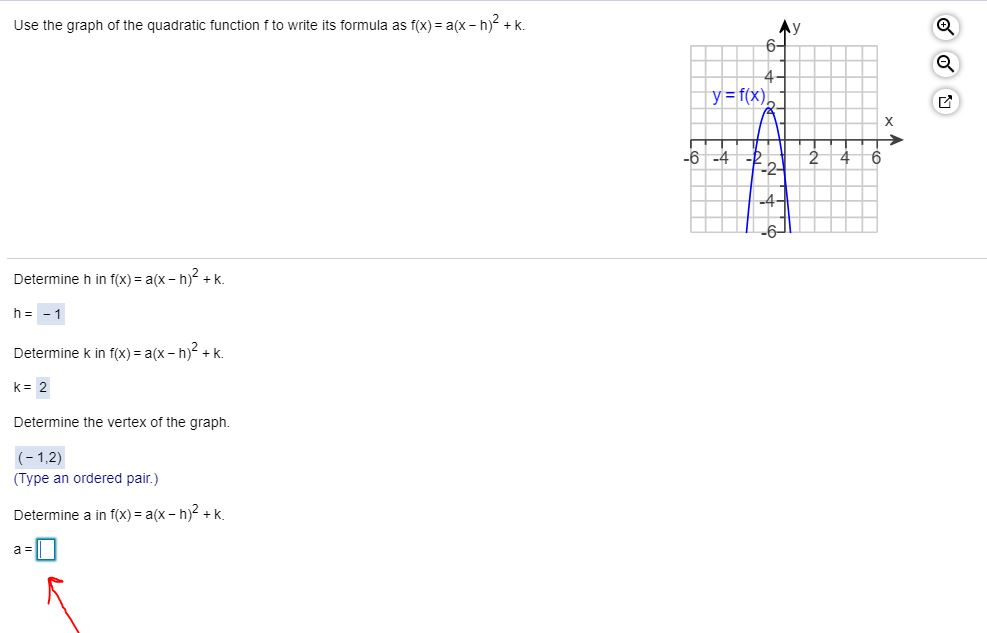
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorThe quadratic function f (x) = a (x h)2 k is in standard form The graph of f (x) = 5 (x 1)2 3 is a parabola that opens , with its vertex at (x, y) = The graph of f (x) = 5 (x 1)2 3 is a parabola that opens , with its vertex at (x, y) = ( )Math Precalculus Precalculus questions and answers Use the graph of the quadratic function f to write its formula as f (x)= a (x h)2 k f (x)= 6 a 4 G 8 14 112 2 24 62
(h, k) and a point on the graph (x, y) to find the general form of the equation of the quadratic function (h, k) = (−5, −1), (x, y) = (−7, 3) f(x) = _____ Found 2Algebra > Quadratic Equations and Parabolas > SOLUTION Write the quadratic function in the form f(x)=a(xh)^2k Then, give the vertex of its graph f(x)=2x^2x52 Log On Quadratics solvers QuadraticsThat would give us X squared minus six X And then I'm gonna put the minus 11 in the back So we need to complete the square by adding something here



2



7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download
F(x) = a(xh)^2k "Get 15% discount on your first 3 ordersC) f(x) = 2(x 3) 2 = 2(x 3)) 2 0 a = 2 , h = 3 and k = 0 The vertex is at (3,0) and it is a minimum point since a is positive Interactive Tutorial Use the html 5 (better viewed using chrome, firefox, IE 9 or above) applet below to explore the graph of a quadratic function in vertex form f(x)=a (xh) 2 k where the coefficients a, hAnswer to Describe the graph of f(x) = a(xh)^2 k when a = 0 Is the graph the same as that of g(x) = ax^2 bxc when a=0?




How To Write Quadratic Functions Video Lesson Transcript Study Com



Parabolas Andymath Com
444 Chapter 8 Graphing Quadratic Functions Graphing y = a(x − h)2 k Graph g(x) = −2(x 2)2 3 Compare the graph to the graph of f (x) = x2 SOLUTION Step 1 Graph the axis of symmetry Because h = −2, graph x =2 −2 Step 2 Plot the vertex Because h = −2 and k = 3, plot (−2, 3) Step 3 Find and plot two more points on the graph Choose two xvalues less than the xcoordinateLearn how to graph just from using the vertex ordered pair and another ordered pair that the graph goes through The graph of a quadratic function is a parabola The general form of a quadratic function is f(x) = ax2 bx c where a, b, and c are real numbers and a ≠ 0 The standard form of a quadratic function is f(x) = a(x − h)2 k The vertex (h, k) is located at h = – b 2a, k = f(h) = f
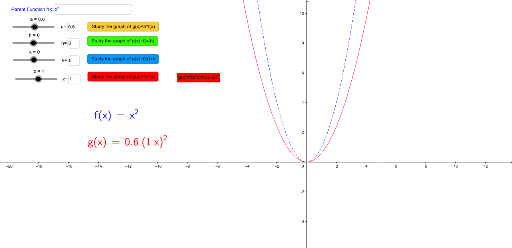



Graph Transformations Discovering Manipulating Functions Geogebra




Describe The Graph Of F X A X H 2 K When A 0 Is The Graph The Same As That Of G X Ax 2 Bx C When A 0 Explain Study Com
Describe what happens to the graph of f (x) = x² when values a, h, and k are different than their usual a=1, h=0, and k=0 in the format f (x) = a (x h)?As f (x) = ax2 bx c (standard form) and g(x) = a(x − h)2 k (vertex form) Quadratic functions can also be written in intercept form, f (x) = a(x − p)(x − q), where a ≠ 0 In this form, the polynomial that defi nes a function is in factored form and the xintercepts of the graph can be easily determined Graphing f (x) = a(x − pQuestion Write the quadratic function in the form f(x)=a(xh)^2k;



1



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora
A vertical stretch or compression a > 0, the parabola opens up and there is a minimum value a< 0, the parabola opens down and there is a maximum value (may also be referred to as a reflection in the xaxis) 1Graph Quadratic Functions Graphs of quadratic functions of the vertex form f(x) = a (x h) 2 k and of the standard form f(x) = a x 2 b x c are presented with several examples and their detailed solutions We start with the graph of the basic quadratic function f(x) = x 2, then we graph examples of quadratic functions in vertex form and then in standard formK and then answer the questions Change in Equation Effect on Graph k positive k negative h positive h negative a negative Tal>1 lakt 3 The discriminant tells you how many and




Vce Mathematical Methods Units 1 And 2 4g Graphing Quadratic Functions




7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip
In general, if you have a parent function, f(x), the graph of a daughter function f(x h) k is related with the graph of the parent function as per these rules The constant h subtracted from the argument, x, translates the graph of the parent function, f(x), h units to the right; The quadratic function f(x) = a(x − h)2 k is in standard form (a) The graph of f is a parabola with vertex (x, y) = (b) If a > 0, the graph of f opens In this case f(h) = k is the value of f (c) If a < 0, the graph of f opens In this case f(h) = k is the value of f please show step by stepThe graph of f(x) = x h k contains the points (6, 2) and (0, 2) The graph has a vertex at (h, 5) Describe how to find the value of h Then, explain how this value translates the graph of the parent function Sample Response The absolute value function is symmetric with its vertex on the line of symmetry Because the points (6, 2



Untitled Document




9 8 Graph Quadratic Functions Using Transformations Mathematics Libretexts
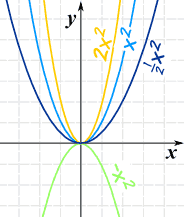
Question Write the quadratic function in the form f(x)=a(xh)^2k Then, give the vertex of its graph f(x)=−2x^212x any help greatly appreciated Answer byThe simplest Quadratic Equation is f (x) = x 2 And its graph is simple too This is the curve f (x) = x2 It is a parabola Now let us see what happens when we introduce the "a" value f (x) = ax2 Larger values of a squash the curve inwards Smaller values of a expand it outwardsExplore the parent graph y=x^3 Experiment with the values of a, h, and k What happens to the graph as these values change?



Graphing Quadratic Functions



Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download
Algebrn _____whose vertex is the point _____The constant k added to the function, f(x), translates the graph of the parent function, f(x), kIf a is negative the graph reflects across the xaxis If a is greater than one, it is a vertical stretch that makes the graph narrower If a is less than one, it is a vertical shrink that makes the graph wider (h, k) is the Vertex of the Quadratic Function h



Www Npsk12 Com Cms Lib Va Centricity Domain 4555 Algebra ii lip 4 Pdf




Parabolas With Functions Of The Form F X A X H 2 K Pages 1 3 Flip Pdf Download Fliphtml5
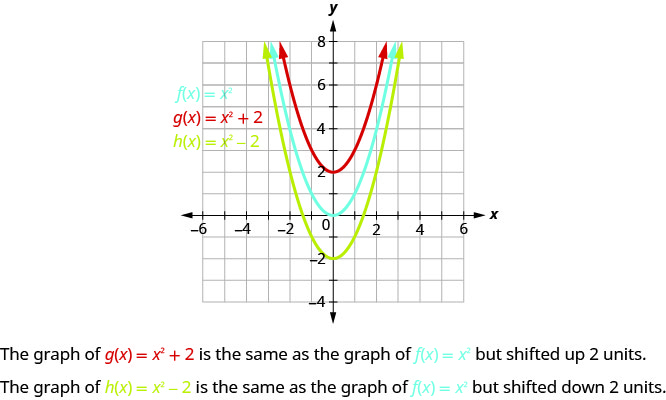
The quadratic function f(x) = a(x h) 2 k, a not equal to zero, is said to be in standard form If a is positive, the graph opens upward, and if a is negative, then it opens downward If a is positive, the graph opens upward, and if a is negative, then it opens downward Example 981 Graph f(x) = x2, g(x) = x2 2, and h(x) = x2 − 2 on the same rectangular coordinate system Describe what effect adding a constant to the function has on the basic parabola Solution Plotting points will help us see the effect of the constants on the basic f(x) = x2 graphExample 960 Graph f(x) = x2 6x 5 by using transformations Solution Step 1 Rewrite the function in f(x) = a(x − h)2 k vertex form by completing the square Separate the x terms from the constant Take half of 6 and then square it to complete the square (1 2 6)2 = 9



Http Www Math Wsu Edu Faculty Dzhang 1fall14 1lecturenotes Fall14 Wed9 10 Pdf




Graphing Quadratic Equations
Question 5918 Complete the square to write the function in f(x) = a(x − h)^2 k form Determine the vertex and the axis of symmetry of the graph of the function f(x) = −4x^2The following graph of f(x) = x2 has been shifted into the form f(x) = (x − h)2 k a parabola with a vertex of 4, negative 2 Mathematics Asked 1 day ago Give Answer Answers V(4,2) In the vertex form, the h value is the x and the k value is the y So if the vertex (4,2) is also (h,k)The x1 you might think shifts the graph to the left but it shifts it to the right So let's just review really quickly what this transformation does y equals half of x xh is a horizontal shift If each is positive it shifts the graph to the right Like when h was one, we had x1 the graph was shifted to the right one unit



Quadratic Functions In The Form Y A X H 2 K Ppt Download




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21
The quadratic function f(x)=a(xh)^{2}k is in standard form (a) The graph of is a parabola with vertex (b) If a>0, the graph of f opens _____ In this caseHow the x or y coordinates is affected?I'm stuck on how I can graph this function for my Algebra class!



Untitled Document




Also Identify The Vertex No Need To Sketch Write The Quadratic Function In A X H 2 K Form Hint Homeworklib
Learn how to graph in vertex form!Since c = 3 > 1, the graph is obtained from that of f(x) = x1/2 by stretching it in the ydirection by a factor of c = 3 Reflection about the x axis The graph of y = f (x) is the graph of y = f (x) reflected about the x axis Here is a picture of the graph of g(x) = (x 2 1) It is obtained from the graph of f(x)Simple and best practice solution for f(x)=a(xh)2k equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so




8 4 Graphing F X A X H 2 K Youtube



Solved Use The Graph Of A Quadratic Function F To Write Its Formula As F X A X H 2 K F X Course Hero
Formula f(x) = a(x h) 2 k The Parabola always produces a "U"shaped graph which can open upwards or downwards depending on the value of "a" Given the values of a, h, and k, fill them into the formula to produce the equation of the graphHow to graph a quadratic function using horizontal shiftsFind the vertex and graph the function (a) f(x)=x^26x (b) f(x)=x^24x1 (c) f(x)=3x^210x2 Answer by stanbon(757) (Show Source)



Solution The Graph Of F X X H K Contains The Points 6 2 And 0 2 The Graph Has A Vertex At H 5 Describe How To Find The Value Of H Then Explain How This Value Translates




Algebra Ii 9 5a Graphs Of F X A X H K Guidelines For Graphing Quadratic Functions Youtube
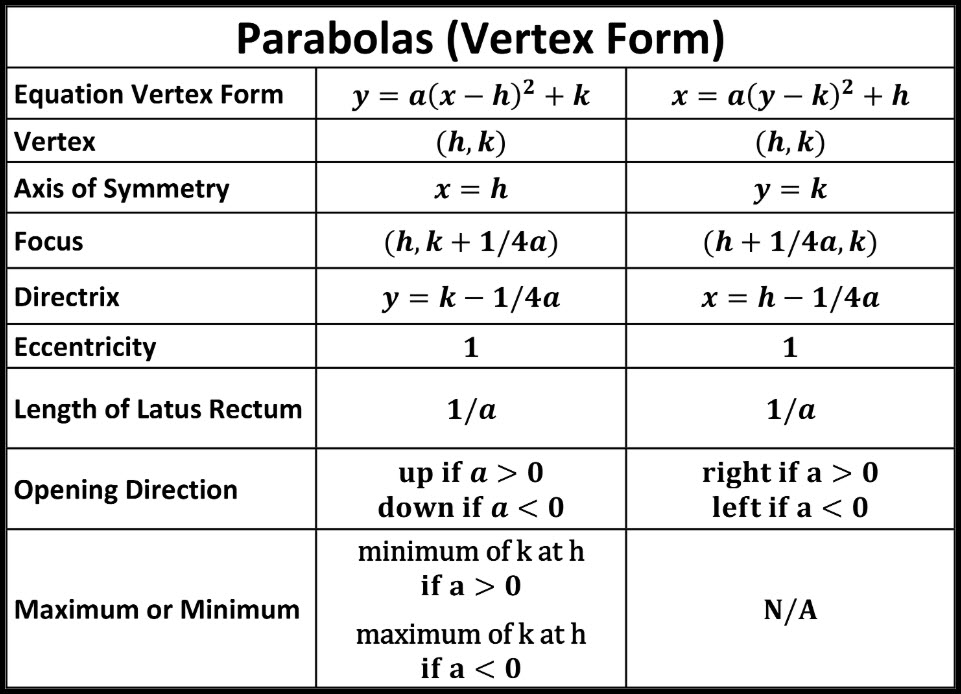
A quadratic function f in vertex form is written as f(x) = a(x h) 2 k where h and k are the x and y coordinates respectively of the vertex (minimum or maximum) point of the graph The graph of of f is a parabola with the vertical line x = h as an axis of symmetryThis video shows how to use vertex form ie y = a(x h)² k to graph a parabola or use it to write an equation from a graph This lesson was created foWhen written in "vertex form "• (h, k) is the vertex of the parabola, and x = h is the axis of symmetry • the h represents a horizontal shift (how far left, or right, the graph has shifted from x = 0) • the k represents a vertical shift (how far up, or down, the graph has shifted from y = 0) • notice that the h value is subtracted in this form, and that the k value is added



Sections 6 And 8 Quadratics Part 2 And Polynomial Functions



Graph Quadratic Functions
A quadratic function in the form f (x) = ax2 bxx f ( x) = a x 2 b x x is in standard form Regardless of the format, the graph of a quadratic function is a parabola The graph of y=x2−4x3 y = x 2 − 4 x 3 The graph of any quadratic equation is always a parabola



1




Quadratic Function




Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown F X Brainly Com




Quadratic Functions Ppt Download
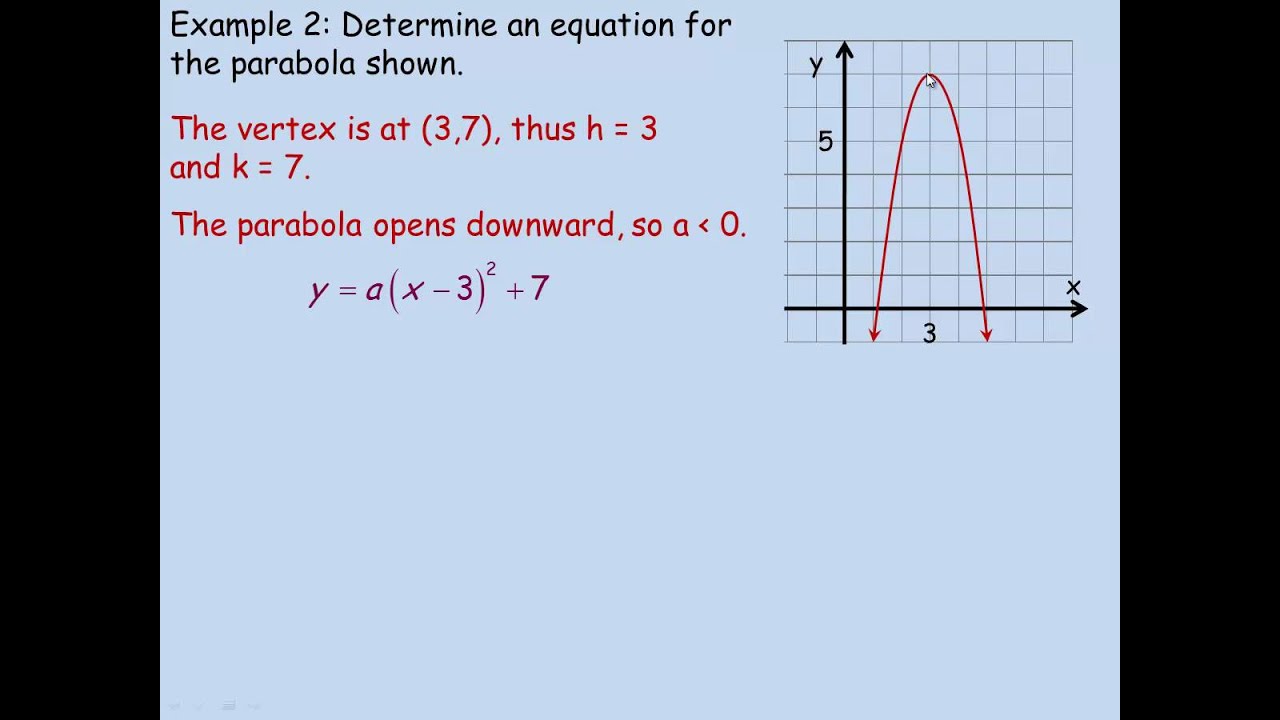



Graphing Y A X H K Youtube



When You Use The Vertex Form Y A X H 2 K What Information Do You Get From A Vertex Form Quora




Vertex Intercept And Standard Form Read Algebra Ck 12 Foundation



7 4 Transforming And Graphing Quadratics And Radicals Intermediate Algebra




Range Of Quadratic Functions Article Khan Academy



Illustrative Mathematics




Write The Quadratic Function In The Form F X Chegg Com
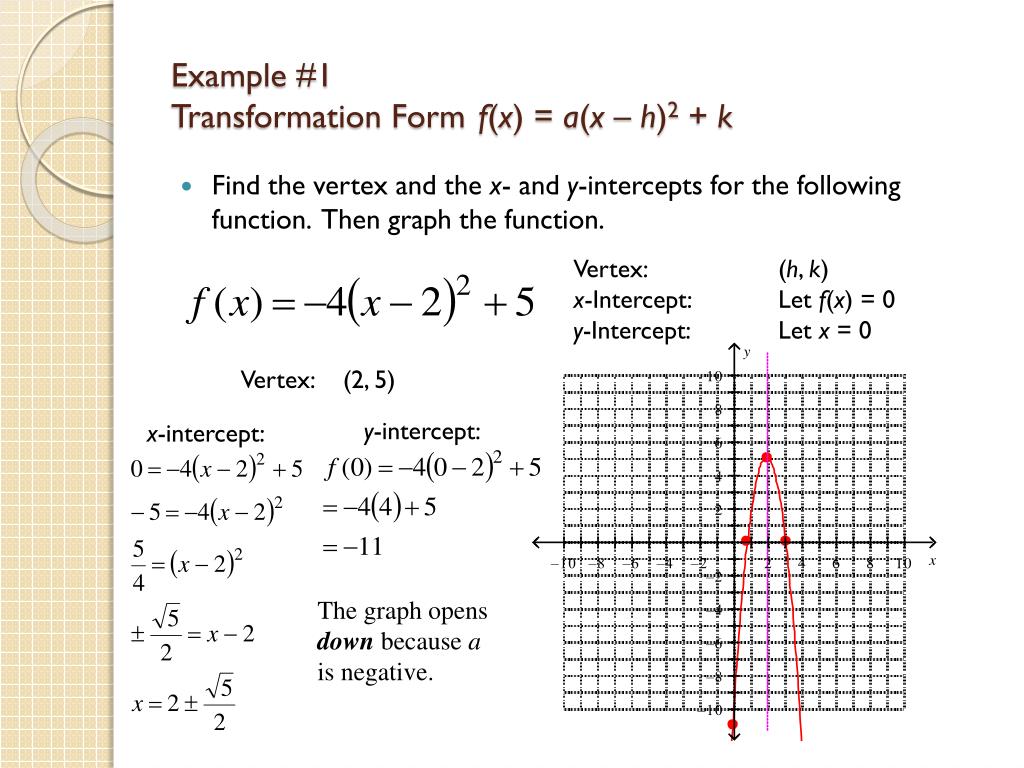



Ppt 3 3 Quadratic Functions Powerpoint Presentation Free Download Id




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21



Staffweb Psdschools Org Eharding Alg1v Bigideasch 8 A1v8 4notesgraphingf A Xh K Pdf



Index Of Ojj Rcm27 Images




Ch 7 Tutoring Notes Quadratics



In The Following Exercises Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown Bartleby




Determine The Quadratic Function Of The Form F X Chegg Com
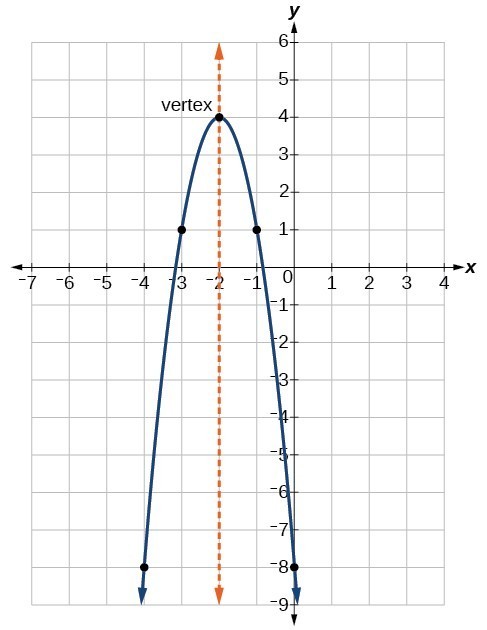



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra




Ppt Quadratics Of The Form Y A X H 2 K Powerpoint Presentation Id



Http Www Daviddelgado Blogsek Es Files 16 09 Qb 14 Math Sl 3 Pdf



Graphing Quadratic Functions



Sections 6 And 8 Quadratics Part 2 And Polynomial Functions



Graphing Quadratic Functions



Q Tbn And9gcsii Oy2yypz9rkmjcuovykbdun8vt6fypixxp7i8sk9 6iuq4 Usqp Cau




Quadratic Functions




Quadratic Formula Calculator




6 6 Analyzing Graphs Of Quadratic Functions



Solved Use The Vertex H K And The Point On The Graph Xy To Find The Standard Form F X A X H 2 K Of This Equation Quadratic Function Course Hero



Polynomial Functions Quadratic Functions Sparknotes



Vertex Form
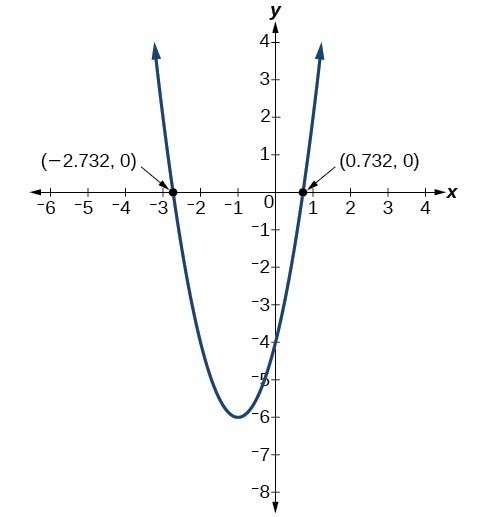



Solve Problems Involving A Quadratic Function S Minimum Or Maximum Value College Algebra




Calgebra A1 8 4 Graphing F X A X H 2 K Youtube



Quadratics Graphing Parabolas Sparknotes




The Graph Of F X X 2 Has Been Shifted Into The Form F X X H 2 K What Is The Value Of H A 1 B Brainly Com



Quadratic Functions



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
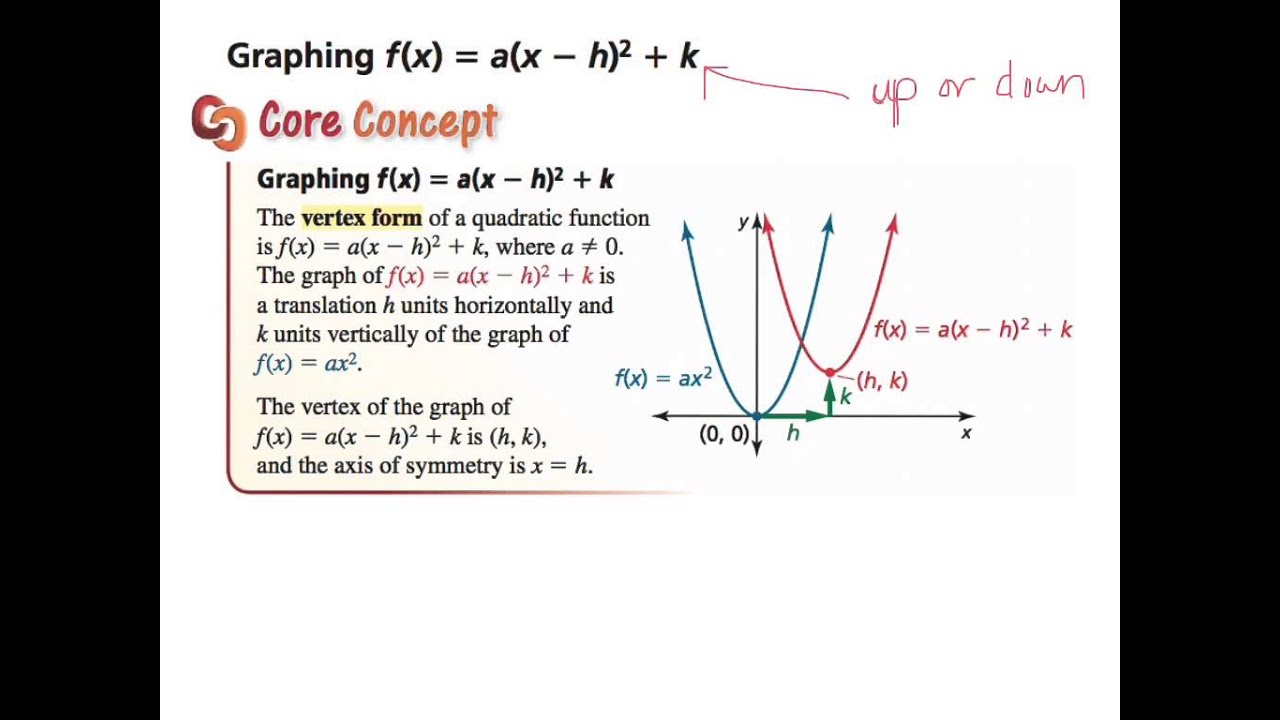



7th Section 8 4 Graphing F X A X H 2 K Youtube



Vertex And Intercepts
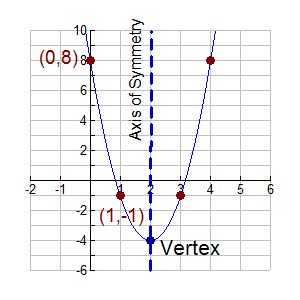



Vertex Form Of Quadratic Equation Mathbitsnotebook A1 Ccss Math




Which Graph Could Be The Graph Of F X X H K If H And K Are Bot




Quadratic Functions



Illustrative Mathematics




Traslacion De Una Funcion Blog De Aula De Pantaleon Hernandez Rodriguez
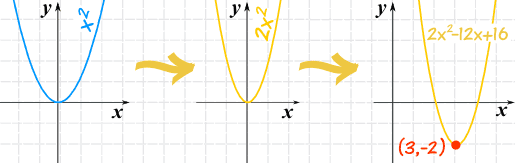



Graphing Quadratic Equations




Unit 5 Quadratic Functions Flashcards Quizlet
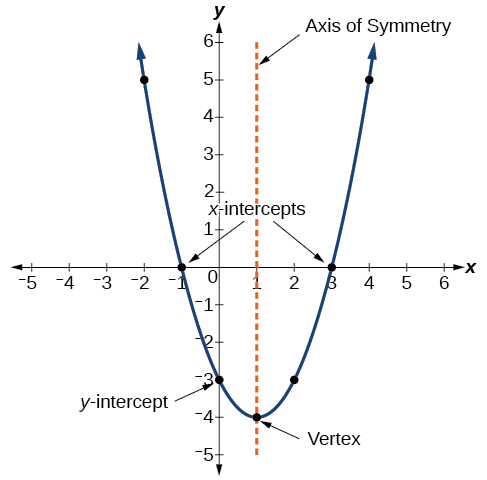



5 2 Quadratic Functions Mathematics Libretexts
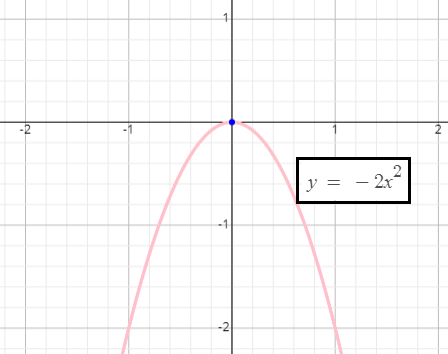



Finding Maximum And Minimum Value Of Quadratic Function
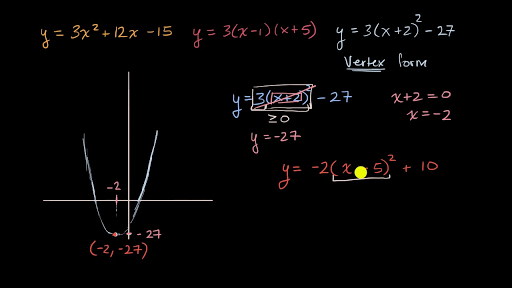



Vertex Form Introduction Video Khan Academy



Solution 2 For The Function Y X2 4x 5 Perform The Following Tasks A Put The Function In The Form Y A X H 2 K Answer Show



Vertex And Intercepts




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube




Quadratic Function Wikipedia




The Graph Of F X Ax 2 All Quadratic Functions Have Graphs Similar To Y X 2 Such Curves Are Called Parabolas They Are U Shaped And Symmetric With Ppt Download
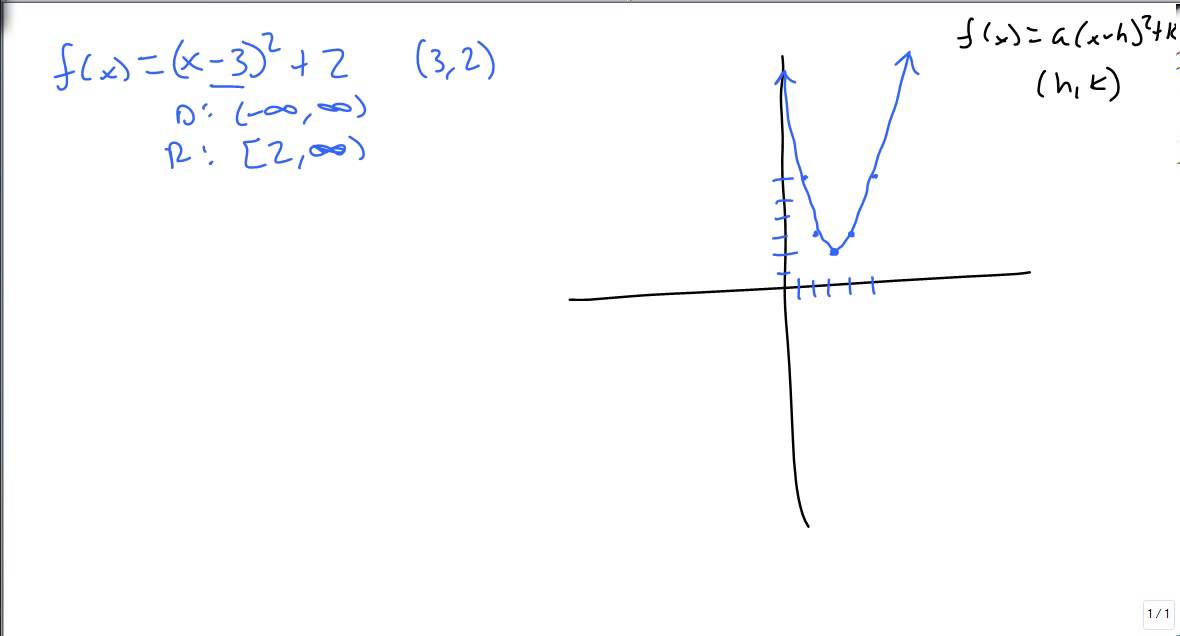



Graph By Transformations F X A X H 2 K Youtube




How To Graph A Quadratic Equation 10 Steps With Pictures
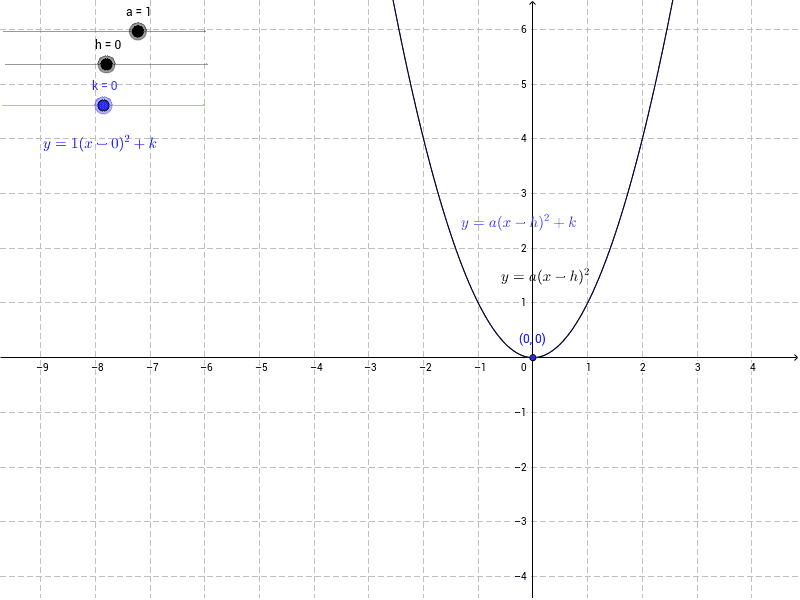



Investigating The Graph Of Y X H 2 K Geogebra



Solution Write The Quadratic Function In The Form F X A X H 2 K Find The Vertex And Graph The Function A F X X 2 6x B F X X 2 4x 1 C F X 3x 2 10x 2



In The Following Exercises Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown Bartleby




Quadratic Function Wikipedia




2 4 Quadratic Functions Ppt Download




Vertex Form Equation Functions Video Lesson Transcript Study Com
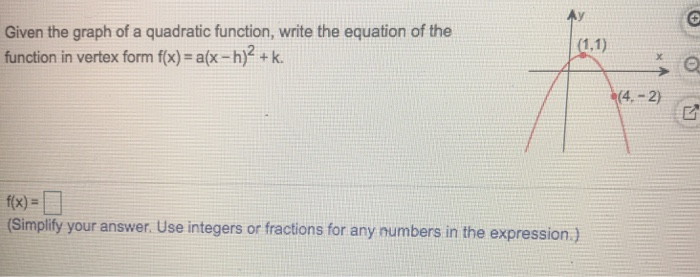



Given The Graph Of A Quadratic Function Write The Chegg Com




Functions In Standard Form Pdf Free Download
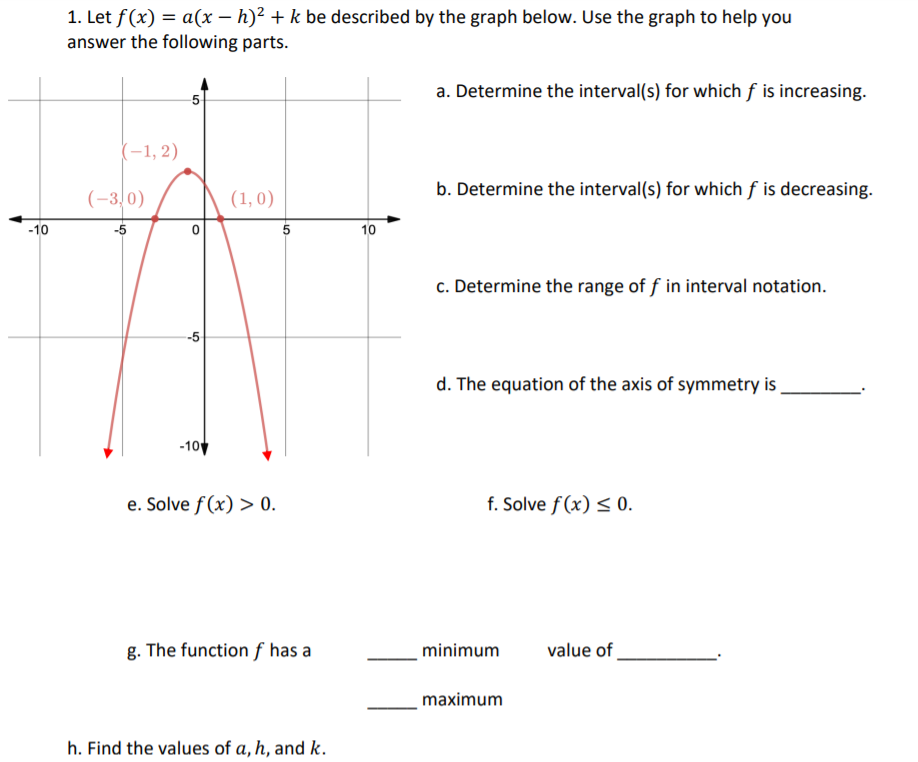



Let F X A X H 2 K Be Described By The Graph Below Chegg Com
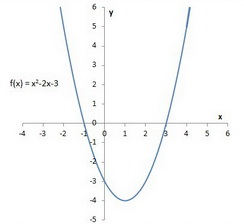



How Do I Convert The Equation F X X 2 2x 3 To Vertex Form Socratic



Http Www Math Tamu Edu Brlynch 150fall17 Notes 150 5 4 Pdf
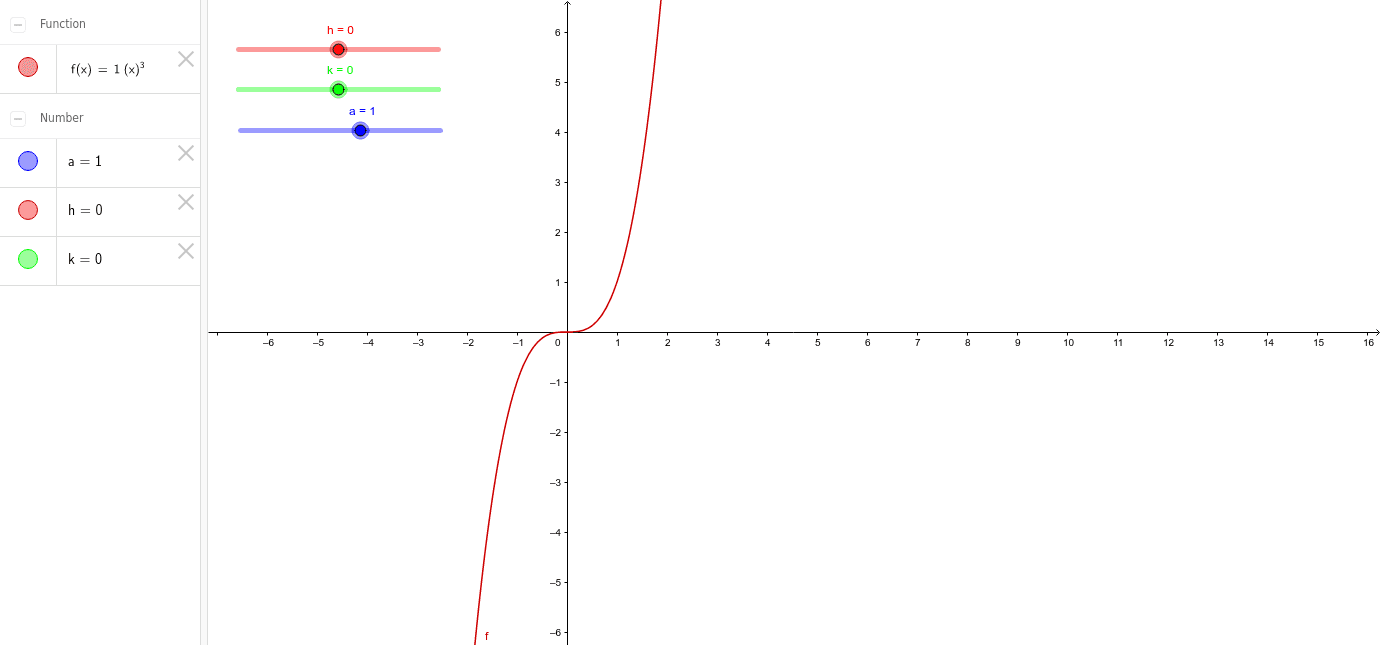



Y A X H 3 K Geogebra



Vertex Form Of A Quadratic Equation Algebra Socratic




Graph F X X H 2 Youtube




The Following Graph Of F X X2 Has Been Shifted Into The Form F X X H 2 K Brainly Com



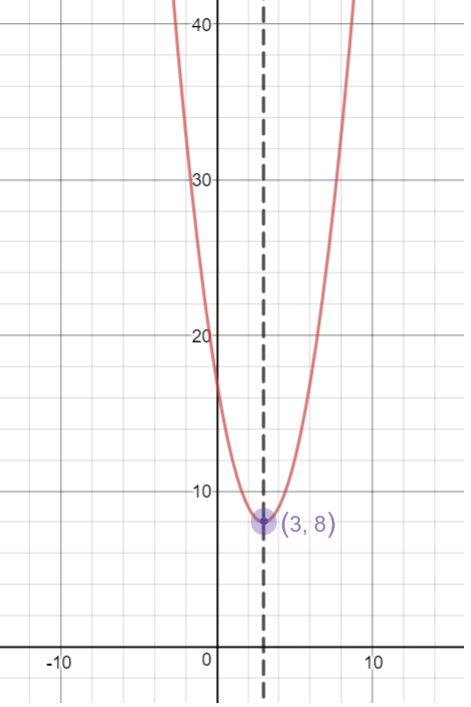
Use The Graph Of The Quadratic Function F To Write Chegg Com
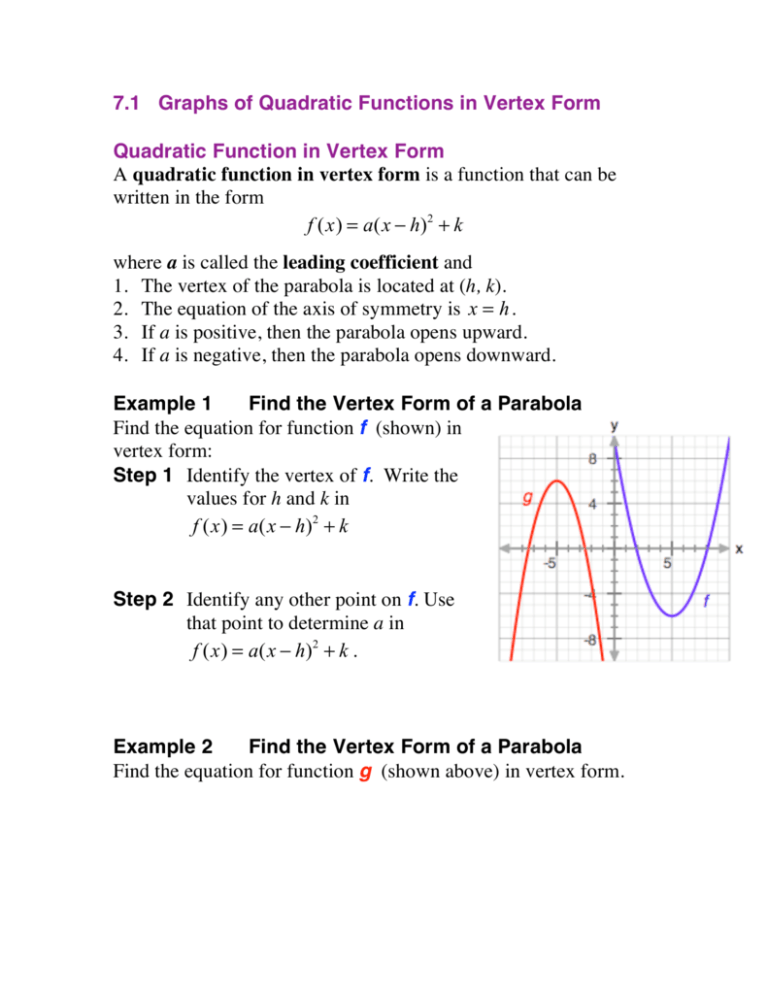



F X A X H 2 K F X A X H 2 K F X A X H 2 K



Illustrative Mathematics



7 4 Transforming And Graphing Quadratics And Radicals Intermediate Algebra
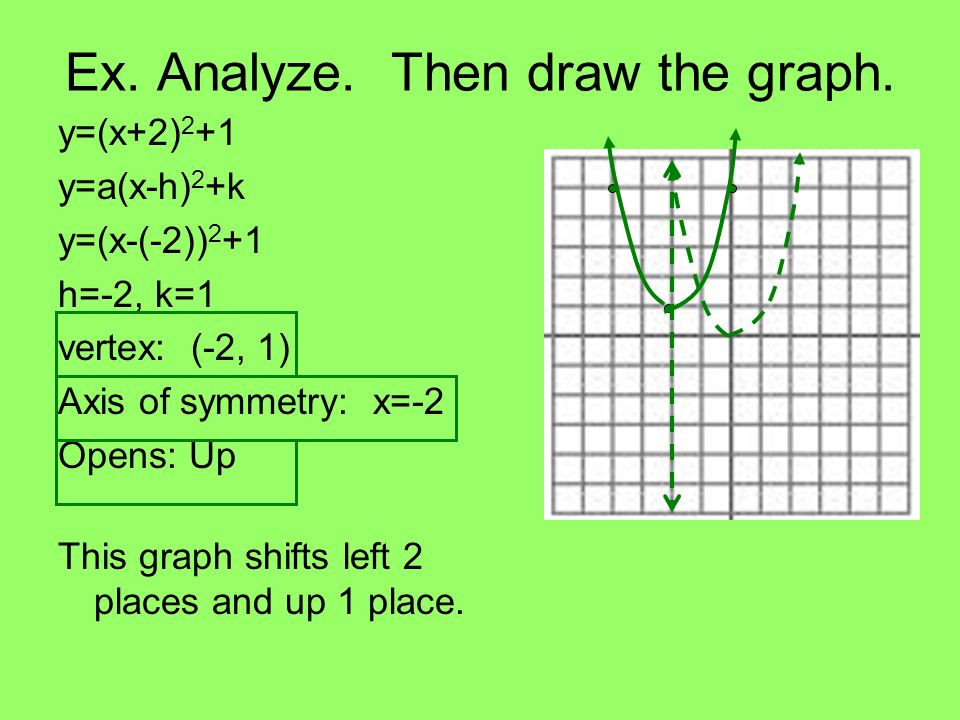



6 6 Analyzing Graphs Of Quadratic Functions Ppt Download



0 件のコメント:
コメントを投稿